Achoimre
Is uirlis bhunúsach mhatamaiticiúil é an chothromóid 1ú céim a úsáidtear chun fadhbanna agus meastóireachtaí laethúla a réiteach, arb é atá ann ná an t -athróg agus na hoibríochtaí feidhmithe a leithlisiú chun a réiteach a fháil.
A Cothromóid 1ú céim Tá sé ar cheann de na coincheapa is tábhachtaí a bhaineann le bun -mhatamaitic agus is féidir é a úsáid chun ríomhaireachtaí éagsúla atá i láthair i gcásanna laethúla a réiteach.
Dealraíonn sé, mar shampla, i dtástálacha scoile nó i measúnuithe tábhachtacha fiú, mar shampla ENEM (Scrúdú Náisiúnta Ardscoil), scrúduithe iontrála, tairiscintí poiblí, i measc rudaí eile.
- Léigh freisin: 12 leideanna chun an comórtas poiblí a rith
Cosúil le foirmlí matamaiticiúla eile, mar shampla an fhoirmle Bhaskara, is féidir an chothromóid 1ú céim a úsáid i gcásanna éagsúla, amhail ríomh costais, pleanáil bealaigh nó réamh -mheastacháin chaiteachais.
Tá sé tábhachtach aird a thabhairt ar shonraí na hoibríochta, amhail comharthaí agus céimeanna an rúin. Ina theannta sin, ba cheart tuiscint a fháil ar na difríochtaí idir cothromóidí an chéad agus an dara céim chun earráidí a sheachaint agus níos mó slándála a bheith acu i rúin.
Cad is cothromóid ann den chéad chéim?
Is éard atá i gcothromóid an chéad chéim ná pianbhreith mhatamaiticiúil a bhaineann le grád anaithnid 1. Léiríonn sé comhionannas agus is é an sprioc an chothromóid seo a réiteach chun luach na hathróg anaithnid a fháil amach.
Is í an fhoirm ghinearálta den chothromóid chéad chéime: Ax + B = 0
Is fíoruimhreacha iad na litreacha “A” agus “B”. Ina theannta sin, is ionann an litir “X” agus an anaithnid atá le fáil. Is féidir aon litir eile a léiriú ar an anaithnid, ach is iondúil gurb iad X, Y agus Z na litreacha is mó a úsáidtear sa chothromóid chun ionadaíocht a dhéanamh ar dhaoine nach bhfuil ar eolas acu.
Ar deireadh, ní féidir leis an líon a léiríonn an litir “A” a bheith nialas i gcothromóid chéad chéime.
- Léigh freisin: Cad a chiallaíonn an chothromóid i uaigh Stephen Hawking
Beidh réiteach i gcónaí ag an gcothromóid chéad chéime, ar a dtugtar fréamh freisin. Mar thoradh ar an toradh, ina dhiaidh sin, déanann an comhionannas ionadaíocht sa chothromóid fíor.
Conas cothromóid 1ú céim a réiteach?
Chun cothromóid 1ú céim a réiteach, ní mór duit roinnt céimeanna a leanúint chun an athróg a leithlisiú agus, tar éis roinnt oibríochtaí matamaiticiúla, an fhréamh a bhaint amach. Tá bealaí éagsúla ann maidir leis seo agus, i measc na gcéimeanna, tá:
- An athróg X nó anaithnid a chuirtear i láthair a leithlisiú;
- Cuir na huimhreacha le hathróg ar thaobh amháin den chothromóid;
- Cuir na huimhreacha ina n -aonar, ar a dtugtar téarmaí neamhspleácha freisin, go dtí an taobh eile den chothromóid, ionas go mbeidh na huimhreacha athraitheacha agus na huimhreacha neamhspleácha scartha ag an tsiombail =;
- Oibríochtaí matamaiticiúla a dhéanamh go dtí go sroicheann sé toradh an anaithnid.
Amharc ar an sampla de réiteach na cothromóide chéad chéim thíos:
2x – 6 = 0
- Agus 6 á gcur leis ar gach taobh den chothromóid, beidh an struchtúr seo a leanas againn: 2x – 6 + 6 = 0 + 6
- Agus oibríochtaí matamaiticiúla á ndéanamh againn, tháinig muid ar 2x = 6;
- Ansin, chun an anaithnid a leithlisiú ní mór duit an dá thaobh a roinnt faoi 2: 2x ÷ 2 = 6 ÷ 2
- Is é an toradh a bheidh air ná x = 3.
Chuige seo, is é fréamh na cothromóide ná 3. Ar an mbealach seo, trí 3 a chur in ionad X, tá an chothromóid fíor:
2. 3 – 6 = 0
6 – 6 = 0
Is éard atá i gceist le réiteach cothromóide ná an t -athróg a leithlisiú agus na téarmaí a atheagrú, chomh maith leis na hoibríochtaí inbhéartacha a chomhlíonadh. Dá bhrí sin, beidh sé indéanta luach beacht an anaithnid a chinneadh. Is féidir an próiseas a dhéanamh le slánuimhreacha, deachúil nó codáin.
Is féidir an chothromóid chéad chéime a réiteach freisin le modh eile, a bhaineann le sainmhíniú an chéad agus an dara ball den chothromóid. Amharc ar an sampla:
5x + 1 = – 9
Sa chás seo, is é 5x + 1 an chéad bhall den chothromóid seo. – 9, ar an taobh eile den tsiombail chomhionannais, is é an dara comhalta den chothromóid ansin.
Le réiteach, is gá an anaithnid a leithlisiú. Ceann de na bealaí is ea an líon anaithnid nach bhfuil ar eolas a chur leis an dara ball, leis an gcúl -oibríocht. Leis sin, beidh:
5x = -9 -1
5x = -10
Tar éis, chun X a leithlisiú, cuir an uimhir a ghabhann leis an dara ball den chothromóid leis an dara ball den chothromóid, leis an gcúl -oibríocht. Chuige sin, in ionad iolraithe (ós rud é go n -iolraíonn 5 an X sa sampla seo), rachaidh sé thar an taobh eile leis an rannán, rud a fhágann go bhfuil:
5x = -10
X = -10 ÷ 5
X = -2
Dá bhrí sin is é fréamh na cothromóide a chuirtear i láthair ná -2.
Samplaí de chothromóidí 1ú céim réitithe
Amharc ar shampla éasca de chothromóid na chéad chéime:
5x = 20
Just a roinnt ar an dá thaobh faoi 5, agus is é an toradh a bheidh air ná: x = 4.
Is sampla é seo de dheacracht idirmheánach sa chothromóid chéad chéime:
5x+4 = 2x – 6
Ar an gcéad dul síos, cuir leis an gcéad bhall na téarmaí le anaithnid agus le saoire, mar an dara ball den chothromóid, téarmaí gan anaithnid. Mar sin beidh:
5x -2x = -6 -4
Ansin déan na ríomhanna a chomhlíonadh chun an fhaisnéis seo a leanas a bhaint amach:
3x = -10
Ar deireadh, trí 3 a rith go dtí an taobh eile tríd an rannán, sroicheann duine an codán -10 / 3.
D’fhéadfadh codán a bheith ag cothromóidí na chéad chéime mar réiteach.
Cothromóidí le lúibíní agus comharthaí a mhalartú
Éilíonn na cothromóidí le lúibíní cheana féin aird a dháileadh, ar oibriú iolraithe idir na huimhreacha taobh amuigh agus taobh istigh de na lúibíní. Mar shampla:
2 (x – 3) = x + 4
Agus an dáileadh á chur i bhfeidhm againn beidh:
2x – 6 = x + 4
Ansin is gá aisiompú anaithnid agus uimhir a dhéanamh chun na heolaithe a aontú mar an chéad bhall agus na huimhreacha a choinneáil mar an dara géag, as a dtagann:
2x – x = +4 +6
Agus na hoibríochtaí á réiteach, sroicheann duine an toradh:
X = 10
Éilíonn cásanna cothromóidí le lúibíní a dteastaíonn malartú comhartha uathu, go háirithe le comharthaí diúltacha roimh lúibíní. De réir mar a théann siad i bhfeidhm ar théarmaí inmheánacha na lúibíní, d’fhéadfadh earráidí sna pointí seo cur isteach ar réiteach.
- Léigh freisin: 3 Modh Simplí le Foghlaim chun Iolrú a dhéanamh gan áireamhán
Iarratais ar chothromóid 1ú céim gach lá
Tá cothromóidí na chéad chéime le feiceáil go minic i gcásanna praiticiúla agus is minic a dhéantar iniúchadh orthu i bhfianaise agus i meastóireachtaí amhail scrúduithe iontrála, nó fiú tástáil enem. Is féidir freisin an chothromóid a chur i bhfeidhm i bhfadhbanna laethúla.
Sampla is ea an chothromóid chéad chéim i ríomh praghsanna. Má chosnaíonn táirge $ 30.00 agus mura bhfuil a fhios ag duine cé mhéad aonad is féidir a cheannach le $ 150.00, is féidir an chothromóid a chóimeáil mar seo a leanas chun a bheith ar an eolas faoi líon na n -aonad is féidir a cheannach leis an luach:
30x = 150
x = 150/30
X = 5 aonad
Is féidir an chothromóid chéad chéime a úsáid freisin chun am a ríomh ar dhíláithriú, nó ar phleanáil ama, mar shampla. Aon uair nach bhfuil aon eolas ann, beidh sé indéanta an chothromóid 1ú céim a úsáid.
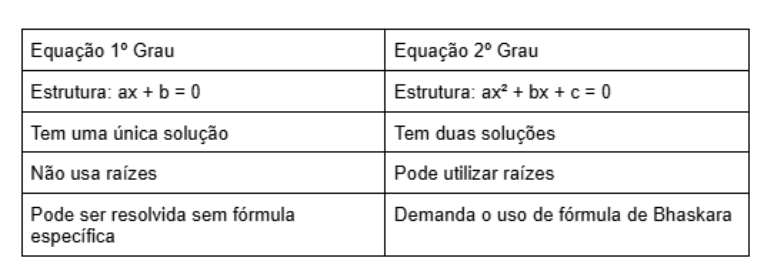
Difríocht idir cothromóid 1ú agus 2ú céim
Tá sé tábhachtach na difríochtaí idir an chéad chéim agus cothromóidí 2ú céim a thuiscint. Sa chéad chás, tá an anaithnid ardaithe go cumhacht 1.
Tá an chearnóg (x²) anaithnid ag na cothromóidí 2ú céim, agus tá straitéisí eile i gceist leis an rún.
Ag an am céanna, d’fhéadfadh dhá fhréamh fíor nó gan aon fhíor -fhréamh a bheith ag an chothromóid 2ú céim.
Earráidí coitianta agus cothromóidí 1ú céim á réiteach
Is botún coitianta é cothromóid 1ú céim a réiteach ná dearmad a dhéanamh ar an gcomhartha a athrú agus téarma á bhogadh go dtí an taobh eile den chothromóid. Dá bhrí sin, nuair a chuirtear uimhir dhearfach ar aghaidh go dtí an taobh eile den tsiombail comhionannais, caithfidh sé a bheith diúltach ar an taobh eile.
Tarlaíonn botún eile go minic sa dáileadh, go háirithe nuair a bhíonn uimhreacha diúltacha i gceist leis. Is gá i gcónaí na téarmaí go léir a iolrú laistigh de na lúibíní agus na rialacha comhartha a bhreathnú.
Conas a fháil amach an cothromóid den chéad chéim é?
Is féidir an chothromóid 1ú céim a fheiceáil nuair a bhíonn an t -athróg 1 easpónant 1 gan a bheith méadaithe faoi athróg eile. Ag an am céanna, má tá an chothromóid le fréamh cearnógach, d’fhéadfadh sé a bheith ina scoil ard.
Cad a chiallaíonn sé chun fréamh na cothromóide a aimsiú?
Is é fréamh na cothromóide luach na hathróg a fhágann go bhfuil an phianbhreith fíor. Ar an mbealach seo, réitítear an chothromóid chéad chéime nuair a fhaightear a fhréamh. Dá bhrí sin, is é an toradh a bhíonn ar fhréamh na cothromóide a aimsiú a fhágann go bhfuil sé fíor.
Mar shampla, i 3x + 6 = 0, is é an fhréamh x = -2, ós rud é, nuair a chuirtear an luach seo in ionad an luach anaithnid sa chothromóid bhunaidh, go bhfaightear an comhionannas.
An bhfuil réiteach ag gach cothromóid 1ú céim?
Tá, tá fíor -réiteach amháin ag gach cothromóid 1ú céim, ar choinníoll go bhfuil an chomhéifeacht athraitheach difriúil ó nialas. Chuige seo, má tá an chothromóid 0x = 5, níl aon réiteach ann agus measfar gur cothromóid neamhbhailí é.
Ar mhaith leat fanacht ar bharr níos mó foirmlí agus leideanna matamaitice eile a chuidíonn leo siúd a chaithfidh staidéar a dhéanamh orthu? Rochtain ar ábhar Terra Educar!